0   引言

湖南省卫星导航定位基准站网(HNCORS)于2015年1月北斗信号加载调试工作全部完成，该系统现有272个基准站，覆盖湖南、贵州两省全域及湖北、江西、广西局部区域，永州市境内有14个基准站，站间平均距离约50 km。该系统能够提供全天候实时厘米级定位；其静态自动解算服务精度可以到毫米，可用于大地测量及高精度变形监测；伪距差分服务改正数据精度能够达到分米级，可用于实时定位、导航和监控等服务。HNCORS基准站分布图如图1所示。

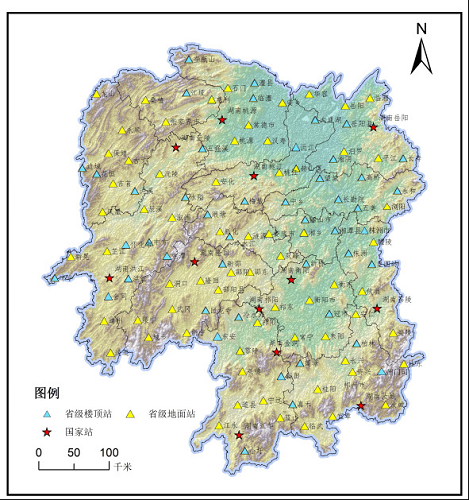
图一  HNCORS基准站分布图

湖南省卫星导航定位基准站网能够提供实时高精度的三维位置定位，但是通过 GNSS测量获得的高程是大地高，需要使用似大地水准面模型进行转换，才能得到我们国家工程项目采用的正常高。建立高精度、高分辨率的似大地水准面模型才能实现高精度的GNSS大地高转换成正常高。满足相应精度的GNSS正常高可以代替传统水准测量。永州市中心城区测绘基准精化工程尚未开展，在永州市中心城区没有高精度的似大地水准面模型，GNSS高程不能直接转换。在小范围地势平坦区域内利用GNSS高程拟合技术对网络RTK采集的实时数据进行高程拟合，结合常规水准测量，确定局部区域的似大地水准面模型从而提高网络RTK数据的正常高精度，提高工作效率，笔者结合永州市河东新城小区排水调查控制测量对这个问题进行了研究。

1   GNSS拟合高程

以大地椭球面为参照面的高程系统称为大地高，以似大地水准面为参照面的高程系统称为正常高，似大地水准面与参考椭球面的距离称为高程异常ζ，其关系为：

H_大地高=H_正常高+ζ              （1）

求解ζ的主要方法有几何法、重力法及组合法等。在一定区域中，当测区中通过GNSS技术获得一部分点的大地高，利用水准联测获得这些点的正常高，可以计算出高程异常。若测区中按照特定密度布设GNSS重合点，求取每个点的高程异常ζ,再应用数学模拟法获得相应的局部似大地水准面模型，最后利用该公式将局部地区的GNSS高程转换为正常高。小范围内我们常常采用几何法进行进行GNSS高程拟合。

2   GPS拟合水准精度评定

为正确客观评定GNSS水准测量精度，在布设几何水准点用于联测时，应尽可能通过布设的水准点去联测相近的GNSS点，外部检核用的起算点也应均匀布置。

2.1  GNSS水准精度评定。用GNSS水准求出的GNSS点间的正常高程之差，在己知点间组成附合或闭合高程导线，再将计算出的闭合差与《国家三、四等水准测量规范》中允许残差进行比较，以衡量GNSS水准达到的精度。

2.2  平面拟合模型的公式为

                    ζ=                  (2)

式中为未知系数，x、y为平面坐标。

            如有N个已知点则V=BX-L                   (3)   

用平差方法，求得模型系数及拟合精度M

                                        （4）

     式中P为已知点高程权值

2.3  二次曲面拟合模型

     假设 x, y为任意一点平面坐标,则其高程异常可表示为:

             ζ                         (5)

式中为ζ的趋势值，为与测区似大地水准面相拟合的数学面,

为误差。

     设：          (6)

     式中为拟合面系数，式(5)、(6)即为二次曲面逼近模型。

2.4  拟合精度按照下式估算：

                      M=                    （7）

式中: v为检核点拟合残差, n为在拟合计算中的总点数。

3  GNSS拟合高程技术应用实例

笔者承担了永州市河东新城小区排水管网雨污水混接调查的测量任务，平面控制测量起算数据为国家三等点，高程控制测量为三等水准。

基于湖南省卫星导航定位基准站网(HNCORS)系统,采用实时动态测量(RTK)方式施测,GNSS接收机平面采集坐标为CGCS2000，精度比较容易达到C级，满足《城市地下管线探测技术规程》（CJJ61-2017）中用于测量地下管线控制点的要求；但是GNSS接收机实时采集的高程为大地高，只能通过HNCORS云服务解算成大地高，相邻控制点间高程精度检验还要依托传统水准测量，耗时耗力。为了提高工作效率，笔者在10km²测区内，采用GNSS高程拟合技术求解正常高，研究GNSS高程拟合技术是否可以在小范围代替传统的几何水准测量。

项目启动后在测区内外依路网均匀布置了18个已知三等水准点，编号SZ1-SZ18,按照项目施策情况在测区内布设了18个GNSS点，编号K1-K18。

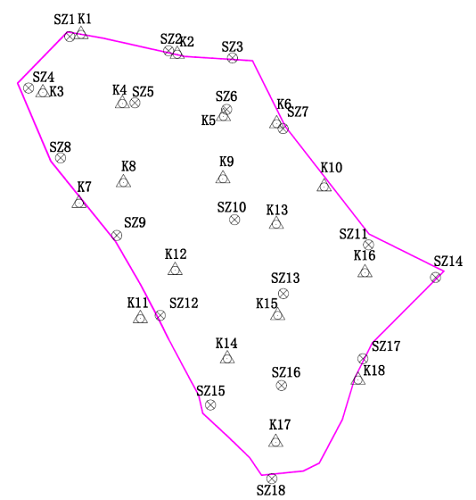
图2  项目GNSS点与水准点分布图

测区均为工业建筑区，地形较为复杂，地势平坦，高差较小。本项目我们选择平面拟合、二次曲面拟合两种方法解算GNSS水准高程。在18个已知三等水准点上架设GNSS接收机，采用静态观测法。通过湖南省卫星导航定位基准站网(HNCORS)静态自动解算服务，将GNSS网整体平差，精度达到了C级网要求，获得可靠的大地高数据。通过解算得到18个水准点的高程异常值。具体数据见表1。

                 表1  水准点坐标、高程异常

K1-K18号点利用湖南省卫星导航定位基准站网(HNCORS),采用GNSS RTK方式施测，根据水准点SZ1-SZ18 的大地高解算这18个点的高程异常，结合平面拟合模型、二次曲面模型，利用最小二乘法求出拟合面系数,从而得到该区域二种拟合法的数学模型，然后再利用两种模型和GNSS RTK测得18个GNSS点的平面位置，确定对应的高程异常值,并结合GNSS实测的该点大地高，利用公式(1),获得该点的正常高。

为检验GNSS拟合高程测量的精度，以18个三等水准点为检核点，K1-K18与临近水准点进行四等水准测量。这样就得到了KZ1-KZ18号点的四等水准的高程值，通过GNSS高程拟合技术计算的正常高和通过湖南省卫星导航定位基准站网(HNCORS)云服务解算的正常高。我们分别用GNSS RTK的正常高减去四等水准的高程值得到的差值、GNSS拟合高程值减去四等水准的高程值得到的差值,结果见表2,图3。

表2  实测值与拟合结果、云解算结果的对比

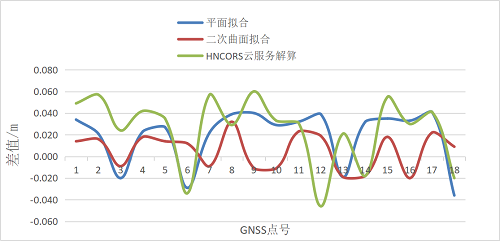
                           图3  差值序列

为综合评定上述几种数据获取方式的精度，这里我们使用统计学中基于加权最小二乘支持向量（WLS-SVM）标准差进行对比分析。各种模型的差值统计特征分析见表3。

                    表3   差值的统计特征

由表3中可以得出本次运用的解算方法中二次曲面拟合标准差最小，各点差值趋于平缓，结合表2中各项数据，二次曲面拟合精度最高，与四等水准高程相比较，最大差值为0.032m,83.3%的拟合高程与四等水准高程差值不超过m。平面拟合高程与四等水准高程相比较，最大差值为0.041m,94.4%的拟合高程与四等水准高程差值不超过m。

4  结 语

    本文为工程的实际应用，通过对测量数据的计算处理我们研究了小区域内GNSS高程拟合的各种计算方法，得出以下结论：

1、不同的拟合方法对高程异常拟合值的影响可以达到厘米级，在高程异常的拟合计算中，必须选择合适的拟合方案。

2、在测区面积较小、地势平坦的情况下，GNSS拟合高程满足《城市地下管线探测技术规程》（CJJ61-2017）中用于测量地下管线控制点的要求，可以达到四等水准限差规定。

3、采用一定数量的已知高等级水准点，通过 GNSS水准的方法，可以提高GNSS RTK数据的高程精度，在一定条件下代替几何水准测量，提高工作效率。

参考文献：

[1] 马云飞、李宏.基于CORS的GPS拟合高程技术在城市管网控制测量中的应用[J].测绘与空间地理信息,2015,38(7):169-171

[2] 李征航，黄劲松．GPS测量与数据处理[M]．武汉：武汉大学出版社，2010

[3] 李春华，黄丁发，罗志才，等.成都市似大地水准面的精化与应用[J].大地测量与地球动力学，2009,29(1)：83-87

[4] 赵辉，张书毕，张秋昭．基于加权总体最小二乘法的GPS高程拟合[J]．大地测量与地球动力学，2011，31(5)：88—91

[5] 任超，梁月吉，蓝岚，庞光锋.不同组合方法对GPS高程拟合的影响[J].大地测量与地球动力学,2015,12(6):1036-1040

[6] CJJ/61-2017.城市地下管线探测技术规程[S].

[7] GB/T 35644-2017地下管线数据获取规程[S].

[8] GB/T 23709-2009区域似大地水准面精化基本技术规定[S].